CURSO RELACIONADO
Física 03
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
2. El coeficiente de fricción estática entre la caja de masa de $3,00 \mathrm{~kg}$ y el plano inclinado de $35,0^{\circ}$ es de 0,300. ¿Cuál es la fuerza mínima $\vec{F}$ perpendicular al plano que debe ser aplicada a la caja para evitar que ésta deslice por la pendiente?
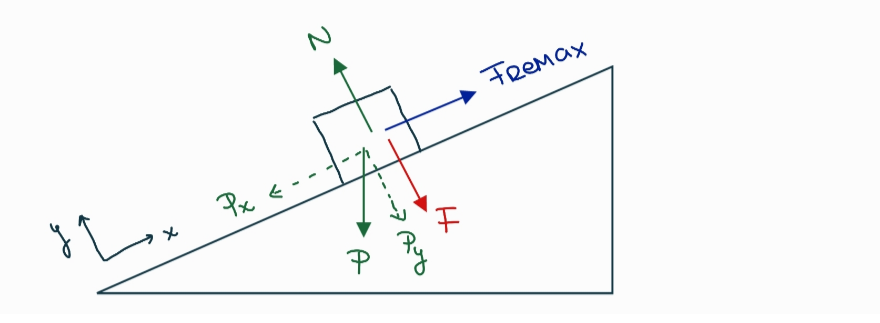
Respuesta
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
